MENENTUKAN PERSAMAAN KUADRAT BARU

Cara menentukan persamaan kuadrat baru – Persamaan kuadrat merupakan sebuah persamaan yang memiliki variabel dengan pangkat tertingginya adalah 2 (dua). Bentuk grafik persamaan kuadrat berupa kurva lengkung yang memiliki satu titik puncak. Titik puncak maksimum terdapat pada kurva yang terbuka ke bawah. Sedangkan titik puncak minimum terdapat pada kurva yang terbuka ke atas.

Bahasan persamaan kuadrat juga sering memuat cara menentukan persamaan kuadrat baru. Jika diketahui sebuah persamaan kuadrat maka kita dapat menentukan persamaan kuadrat baru dengan akar – akar yang berbeda. Melalui postingan ini, kita akan mempelajari cara menentukan persamaan kuadrat baru dari persamaan kuadrat awal yang diketahui.

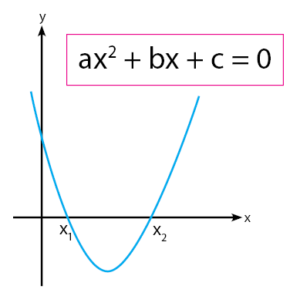
Cara menentukan persamaan kuadrat baru dapat memanfaatkan rumus penjumlahan akar – akar persamaan kuadrat dan hasil kali akar – akar persamaan kuadrat. Bagaimana caranya? kita akan mencari tahu jawabannya. Pada bagian akhir akan diberikan contoh soal menentukan persamaan kuadrat baru.

Pembahasan di sini adalah seputar rumus hasil jumlah dan perkalian akar-akar persamaan kuadrat dengan memanfaatkan koefisen dari persamaan kuadrat. Rumus ini diperoleh dengan memanfaatkan rumus abc, sebagai salah satu cara untuk menentukan akar-akar persamaan kuadrat. Hasil akhirnya akan diperoleh rumus umum untuk mengetahui jumlah dan perkalian dari akar-akar persamaan kuadrat. 

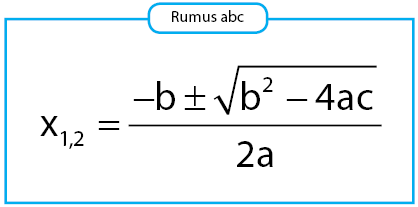
Berikut ini adalah rumus jumlah dan hasil kali akar-akar persamaan kuadrat.

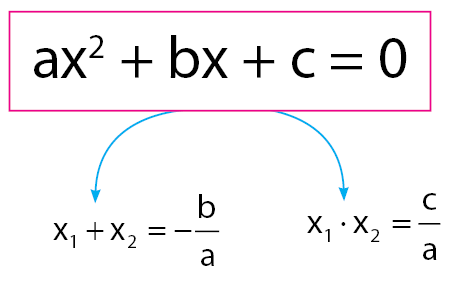
Persamaan yang dapat digunakan untuk menentukan persamaan kuadrat baru adalah sebagai berikut.

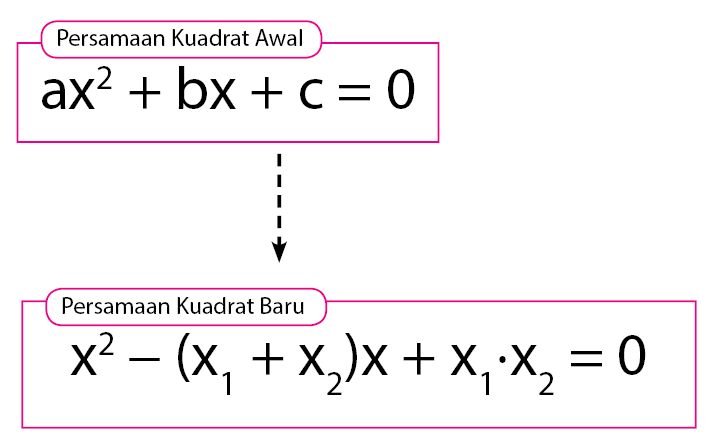
Dengan x₁ dan x₂ merupakan akar – akar dari persamaan kuadrat awal.

Langkah – langkah menentukan persamaan kuadrat baru:

1. Menentukan jumlah dan perkalian akar-akar dari persamaan kuadrat awal.
2. Menentukan jumlah dan perkalian akar-akar persamaan kuadrat baru yang diketahui.
3. Membentuk persamaan kuadrat baru sesuai dengan rumus yang telah diberikan di atas:
   x² – (x₁ + x₂)x + x₁ ⋅ x₂ = 0

Berikutnya akan diberikan contoh soal cara menentukan persamaan kuadrat baru berserta dengan pembahasannya. Simak pada ulasan di bawah.

Contoh Soal dan Pembahasan

Pada ulasan di atas, telah diberikan rumus-rumus yang dapat digunakan untuk menentukan persamaan kuadrat baru. Berikutnya akan diberikan contoh soal dan pembahasan cara menentukan persamaan kuadrat baru untuk menambah pemahaman Anda. Simak contoh soal beserta pembahasan menentukan persamaan kuadrat baru di bawah.

Contoh 1 – Soal Menentukan Persamaan Kuadrat Baru

Diketahui akar – akar persamaan kuadrat x² + 2x + 3 = 0 adalah α dan β. Persamaan kuadrat baru yang akar – akarnya adalah (α – 2) dan (β – 2) adalah ….
A. x² + 6x + 5 = 0
B. x² + 6x + 7 = 0
C. x² + 6x + 11 = 0
D. x² – 2x + 3 = 0
E. x² + 2x + 11 = 0

Pembahasan:

Berdasarkan persamaan kuadrat x² + 2x + 3 = 0, dapat diketahui bahwa:

Jumlah akar-akar persamaan kuadrat:

   

   

   

Perkalian akar-akar persamaan kuadrat:

   

   

Untuk persamaan kuadrat baru, maka:

Jumlah akar – akar persamaan kuadrat:

(α – 2) + (β – 2) = α + β – 4
= –2 – 4
= –6

Hasil kali perkalian akar-akar persamaan kuadrat:

(α – 2)(β – 2) = αβ – 2α – 2β + 4
= αβ – 2(α +β) + 4
= 3 – 2(–2) + 4
= 3 + 4 + 4
= 11

Jadi, persamaan kuadrat baru yang akar – akarnya adalah (α – 2) dan (β – 2) adalah

x² – ( x₁ + x₂ )x + ( x₁ ⋅ x₂) = 0
x² – ( – 6)x + 11 = 0
x² + 6x + 11 = 0

Selain cara runut yang telah diberikan seperti di atas, terdapat cara cepat menentukan persamaan kuadrat untuk bentuk soal seperti di atas. Simak caranya pada langkah-langkah di bawah.

RUMUS CEPAT

Perhatikan bahwa akar-akar persamaan kuadrat baru memiliki pengurangan nilai yang sama, yaitu –2. Untuk menentukan persamaan kuadrat baru dalam kasus soal seperti ini dapat dilakukan dengan substitusi invers nilai persamaan kuadrat baru ke persamaan kuadrat awal. Perhatikan cara-caranya seperti berikut ini.

Invers dari ( x – 2) adalah ( x + 2), substitusi nilai inversnya ke persamaan kuadrat awal seperti berikut ini.

( x + 2)² + 2( x + 2) + 3 = 0
x² + 4x + 4 + 2x + 4 + 3 = 0
x² + 6x + 11 = 0

Hasil yang diperoleh sama dengan cara sebelumnya, bukan? Tapi cara cepat menentukan persamaan kuadrat ini hanya dapat digunakan saat akar – akar persamaan kuadrat baru memiliki pengurangan atau penjumlahan yang sama.

Jawaban: C

Contoh 2 – Menentukan Persamaan Kuadrat Baru

Persamaan kuadrat x² – 5x + 2 = 0 mempunyai akar – akar α dan β. Persamaan kuadrat yang akar – akarnya α² dan β² adalah ….
A. x² – 21x + 4 = 0
B. x² + 21x + 4 = 0
C. x² + 21x – 4 = 0
D. x² – 21x – 4 = 0
E. – x² – 21x + 4 = 0

Pembahasan:

Berdasarkan persamaan kuadrat x² – 5x + 2 = 0 dapat diperoleh:

α + β = 5
α ⋅ β = 2

Sehingga,

Jumlahan akar – akar baru:
α² + β² = (α + β)² – 2αβ
= 5² – 2(2)
= 25 – 4
= 21

Hasil kali akar – akar baru:
α² ⋅ β² = (αβ)²
= 2²
= 4

Sehingga, persamaan kuadrat barunya adalah x² – 21x + 4 = 0.

Jawaban: A

Contoh 3 – Menentukan Persamaan Kuadrat Baru

Jika α dan β merupakan akar – akar dari persamaan kuadrat x² – x + 3 = 0, persamaan kuadrat baru yang akar-akarnya α² – α dan β² – β adalah ….
A. x² – 6x + 9 = 0
B. x² + 6x + 9 = 0
C. x² + 6x – 9 = 0
D. x² – 6x – 9 = 0
E. -x² + 6x + 9 = 0

Pembahasan:

Dari persamaan kuadrat: x² – x + 3 = 0
α + β = 1
αβ = 3

Jumlah akar – akar baru:

α² – α + β² – β = α² + β² – α – β
= (α + β)² – 2αβ  – (α + β)
= 1² – 2 ⋅ 3 – 1
= 1 – 6 – 1
= – 6

Perkalian akar-akar baru:

(α² – α)(β² – β) = (αβ)^{2} – αβ(α + β) + αβ
= 3² – 3(1) + 3
= 9

Jadi, persamaan kuadrat barunya adalah x² + 6x + 9 = 0.

Jawaban: B

Demikianlah tadi ulasan cara menentukan persamaan kuadrat baru serta contoh soal cara menentukan persamaan kuadrat baru dengan pembahasannya. Terimakasih, semoga bermanfaat.